Prime numbers had always been there in the background of my schooling, but they never lit up for me until I began to see them as something more than arithmetic drills.
While doing a science lesson with my children, we read about how early philosophers believed atoms were the indivisible building blocks of reality, a theory that held until modern science finally split them apart. That image made primes suddenly feel alive to me, not just arithmetic curiosities, but numbers standing alone as the unbreakable foundation of mathematics.
My mind has never been quick with rote facts. Multiplication tables, for example, slipped past me when I was young, not because I wasn’t trying, but because I kept straining after the pattern beneath. Things take their time to settle, sometimes for years, but when they do, they do not sit shallowly. They sink deep, like water finding hidden roots. Primes only opened themselves to me in this way when I could see them not as columns on a chart, but as building blocks of reality, carrying weight far beyond the classroom.
From there, the connections spread. If atoms were once thought indivisible, and primes still are, what does that say about the deeper structure of reality. Thomas Aquinas’s cosmological argument from efficient cause has always drawn me, the idea that every effect needs a cause, leading ultimately to a first cause that itself has no cause. Primes feel like a numerical reflection of that same impulse, the need for a foundation. Numbers themselves invite that same search, as if they are asking what lies beneath their surface. Nowhere is this more striking than with the primes.
The prime counting function rose out of this curiosity. Mathematicians asked a simple question: how many primes are there below a given number x. The answer, π(x), rises step by step like a jagged staircase. Sometimes the steps are tight, sometimes they stretch wide, and no one could see a rhythm in their spacing.
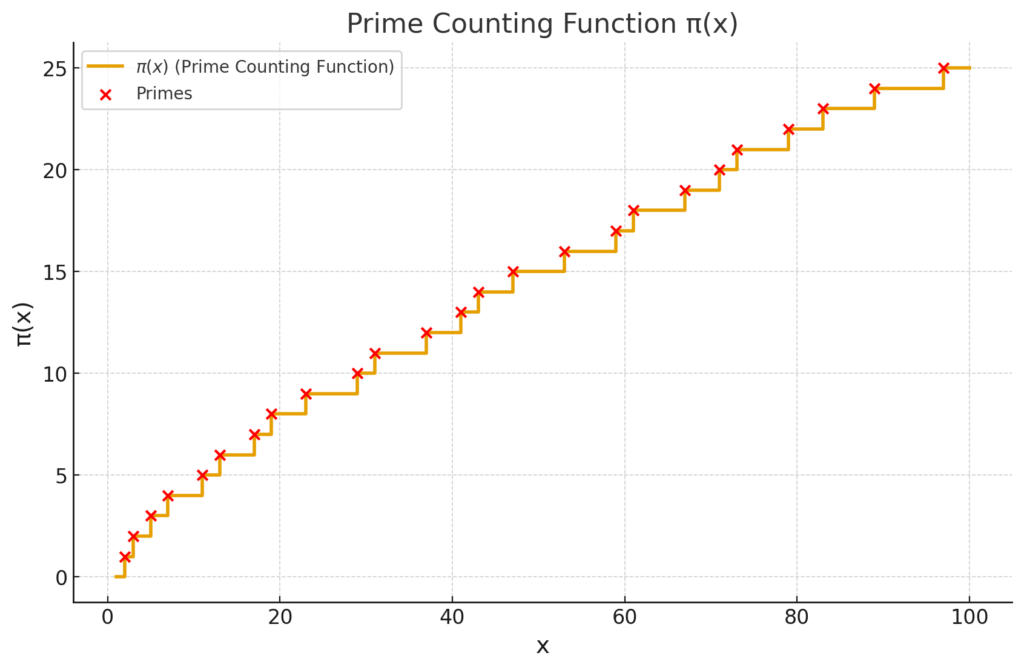
In the early 1800s, a young German mathematician named Carl Friedrich Gauss studied this staircase closely. Still only a teenager, he noticed that it seemed to follow a pattern. He suggested a new function, x divided by the logarithm of x, which grows more slowly than x alone. This slowing captures how primes thin out as numbers get larger, giving a surprisingly close estimate to the true staircase.
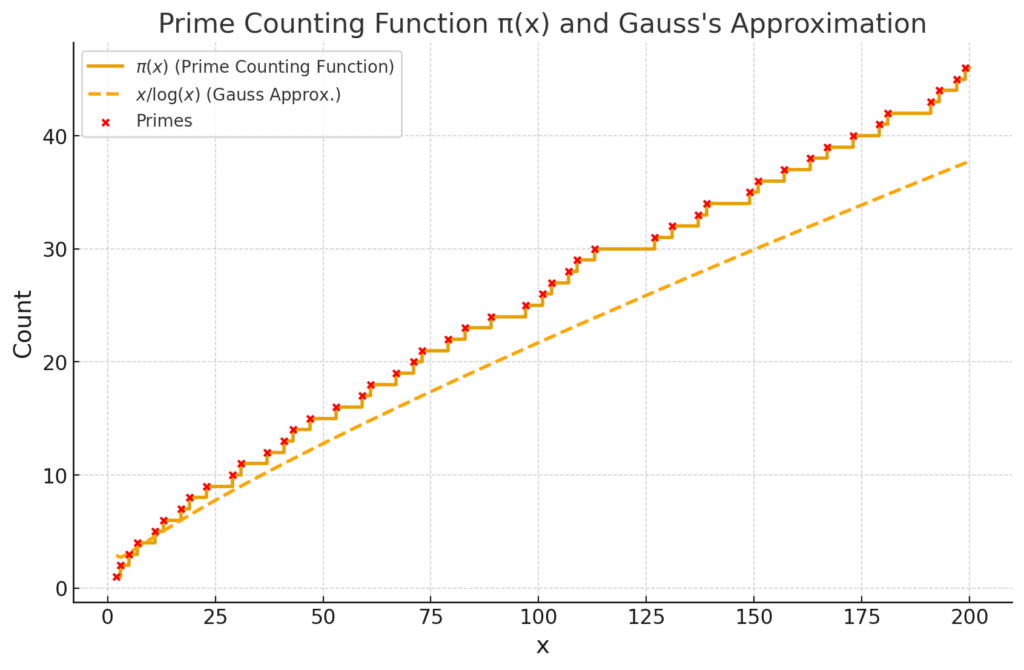
Others tried to draw smoother curves to fit it, but no matter how close they came, the irregularities remained. The staircase stood as a stubborn mystery, waiting for a deeper explanation.
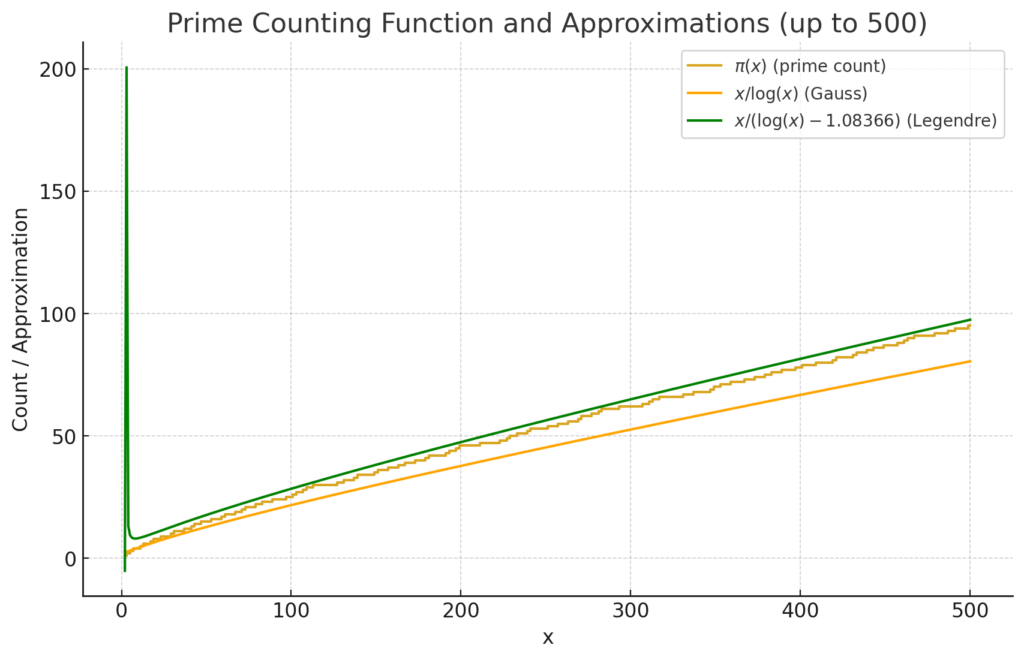
Mathematicians began to shift focus: instead of searching for a better curve, they studied the error itself, the back-and-forth oscillations between the staircase and Gauss’s line.
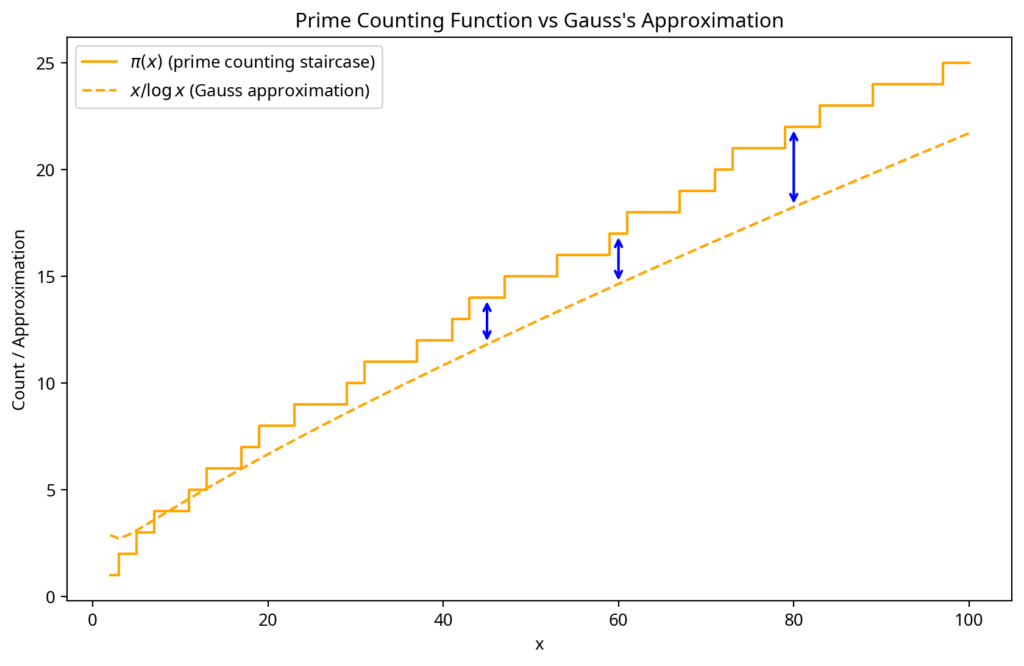
Then, in 1859, a quiet mathematician named Bernhard Riemann stepped into the puzzle. Others had tried to smooth the staircase with better curves, but the stubborn oscillations between the steps and Gauss’s line remained. Riemann suggested that these irregularities might not be random at all, but shaped by something deeper, a hidden pattern that lived not on the number line itself, but in a new landscape of mathematics.
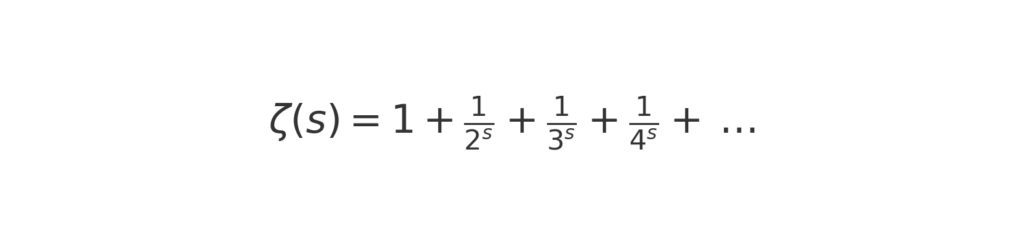
The zeta function first appeared as a humble series, each natural number set in the denominator, the terms growing smaller as they advanced. For inputs greater than one, these fragments knit themselves into a finite sum, a surprising order born out of endless addition.
When the input is two, the sum folds back into geometry itself, astonishingly equaling π²/6, as if circles were whispering their presence inside arithmetic.
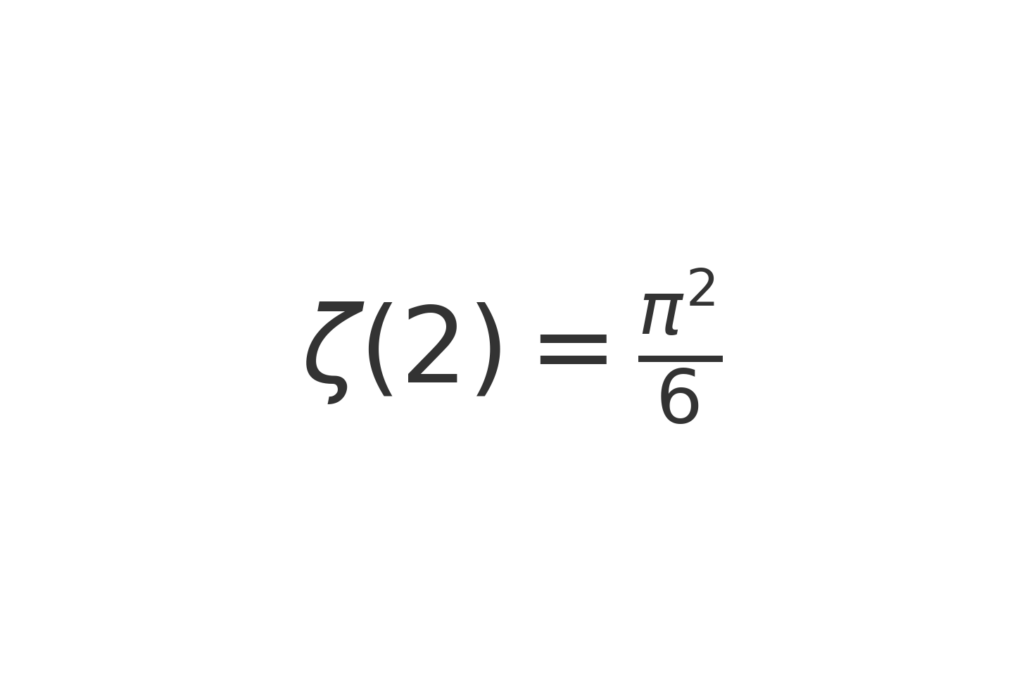
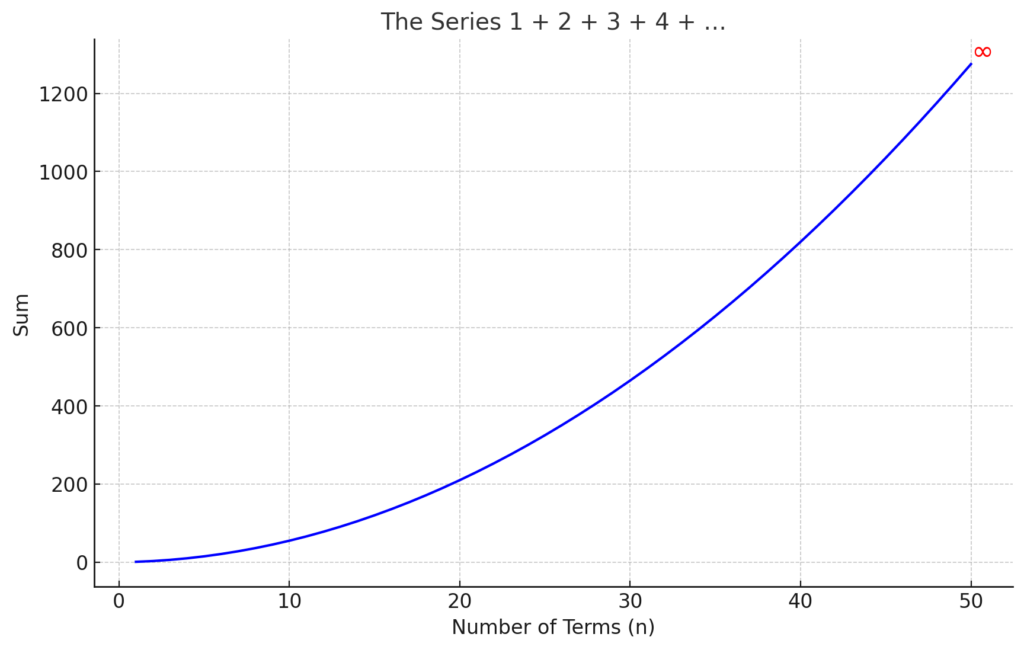
And when s equals minus one, the series tries to gather all the natural numbers together, racing off toward infinity. At first it looks hopeless, but later mathematicians showed that by extending the zeta function, this impossible sum could be assigned a precise value, one that astonishingly connects back to the physical universe.
Mathematics had long lived on the number line, stretching left and right without end. But the zeta function pushed beyond that line into a broader landscape: the complex plane. Here, every number is no longer just a single mark along the line, but a point on a sheet. Each point has two directions to it — one that runs left and right like real numbers, and another that rises and falls like a hidden dimension. This extra axis was strange at first, because it was not built from real numbers but from a new kind, later called imaginary. Only after creating this two-dimensional world could the zeta function show its full form.
The zeta function, though, carried more than this fragile facade. A century earlier, Leonhard Euler had shown that the simple sum could also be written as a product built entirely from the primes. It was the first suggestion that the secret rhythm of the primes might be hidden within the zeta function itself.
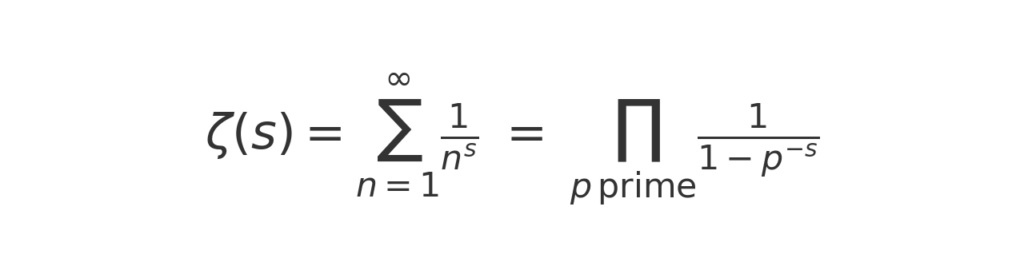
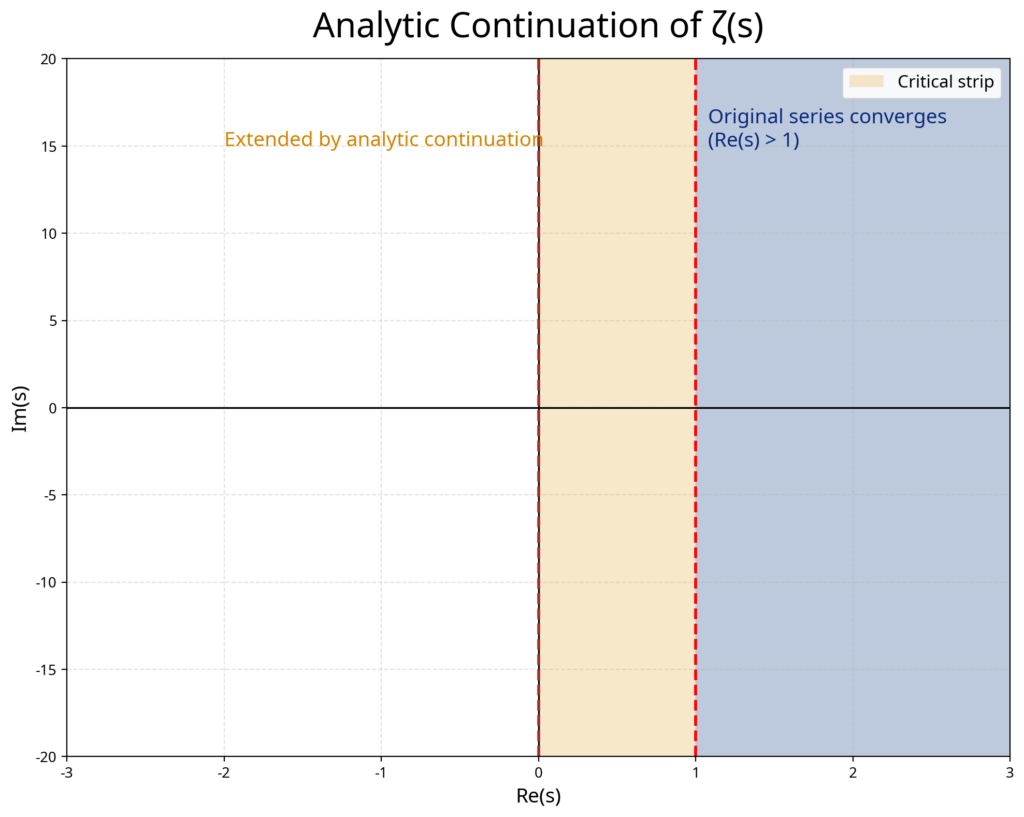
The zeta function does more than generate surprising values. It also carries within it certain points where it collapses to zero. These are called the zeros of the zeta function, and they hold the key to the mystery of the primes. Some of them lie at the negative even numbers and are called trivial zeros. But the others, the so-called nontrivial zeros, live in the critical strip, the region where the real part of s lies between zero and one. The great claim of the Riemann Hypothesis is that every one of those nontrivial zeros falls exactly on the critical line, where the real part of s equals one-half.
On this larger canvas the zeta function reveals its hidden life, extending far beyond the narrow band of the real numbers, though it breaks down at one, where the function cannot be defined. Analytic continuation is the mathematician’s way of carrying the zeta function into this wider world. The original series only converges—meaning it settles down to a finite value—when the real part of s is greater than 1. For other values, the series diverges—racing off toward infinity without ever landing anywhere. Analytic continuation extends the function across the complex plane, assigning values even where the series itself would normally fail to make sense. This is why ζ(−1) is not taken from the raw sum one plus two plus three and so on, which really does run off to infinity. Instead, it emerges from the continuation of the function, which stretches unbroken into that region. Under this broader definition, ζ(−1) takes the value −1/12.
At first this seems like nonsense. How could the sum of all natural numbers equal a negative fraction. But here is where mathematics and physics shake hands. That strange value appears in string theory, where the vibrations of tiny strings naturally call up the divergent series 1 + 2 + 3 + 4 + …, and only by using ζ(−1) = −1/12 do the equations make physical sense. The same happens in quantum field theory, where the Casimir effect has been tested in the lab: two metal plates placed close together in a vacuum are pushed toward each other, not by any visible force, but by the restless energy of empty space itself. The calculation that predicts that force depends on assigning meaning to the divergent sum through the zeta function.
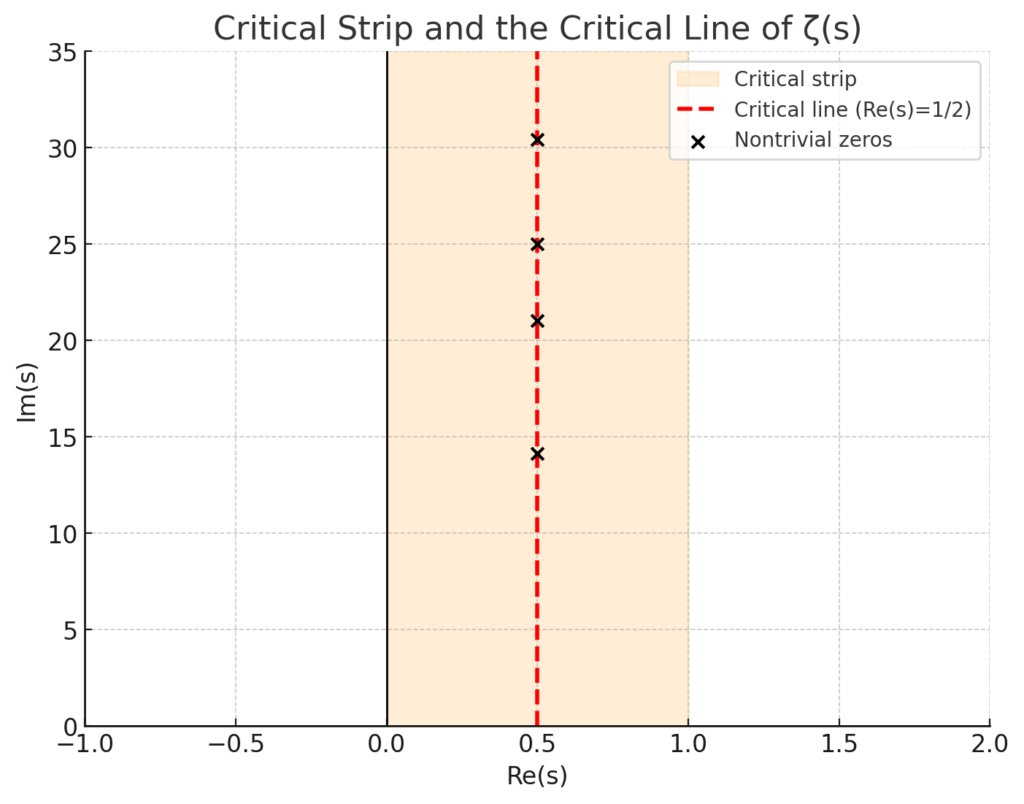
And the connection runs deeper still. The nontrivial zeros of the zeta function, arrayed within the critical strip, share the same statistical patterns as quantum energy levels in chaotic systems. What first appeared in pure mathematics later echoed in physics experiments, where the spectra of certain quantum systems mirrored the hidden spacing of the zeros. It is as if the music of the primes is being played both in the integers and in the quantum realm, two worlds joined by the same rhythm.
This is why the hypothesis matters so deeply. Countless theorems across number theory and beyond rest upon it, like beams leaning on an untested pillar. It is one of the great frontiers of mathematics, with even a million-dollar prize set aside for whoever can resolve it. To prove or disprove it would be to hear, at last, whether the music of the primes resolves into harmony or slips into dissonance, whether the rhythm that has guided mathematics for centuries is order or illusion.Primes, atoms, first causes, quantum vacuums, they all circle back to the same mystery. What looks simple or random at first often conceals a deeper order, one that both reveals and unsettles. Even the strongest structures may fracture, but in the fracture something else is glimpsed, a reality stranger and more subtle than we imagined. Truth is like that, often hidden, often stranger than we expect, but never nothing. Just as primes quietly undergird every number, and just as the vacuum itself is never empty, truth endures even when it looks fractured.